An Investigation into the Price of Goo

Jonathan Searcy, 20 October 2022

Introduction

I had been wondering over the past few years what drives the prices of assets of a certain class. These assets are difficult, if not impossible to value in a fundamental sense, but perhaps attractive because there is no immediately apparent end to their growth trajectory, at least in the sense of their prices. I would include in this asset class virtually all cryptocurrencies and the shares of at least a few American technology companies.

In an effort to understand the market dynamics of these kinds of assets, I undertook an investigation into the effect of supply and demand in a market for a globally finite amount of a notional commodity, goo, the quantity of which is measured in globs, that is neither created nor consumed, but is generally considered more desirable than cash except in circumstances in which the cash available to an individual is uncomfortably low, in which case cash is more desirable.

I accomplished the investigation with a computer model that emulates a population of individuals, called bots, who buy or sell goo depending on their economic circumstances. If you would like to experiment with the model itself, it is here. Note that consecutive runs of the model produce slightly different results as a consequence of the run-dependent random number steams that decide the probabilistic outcomes.

Behaviour of a Bot

In the model of the population of bots, each bot has a balance of cash and a balance of goo, which are initialised and managed in accordance with the requirements of the various experiments described in the following sections.

The model emulates the processing of individual transactions. Transactions such as the handouts mentioned in the next section are scheduled to happen at a particular instant in time. Scheduled transactions are put in a queue ordered by the time of the transaction. The model processes transactions in time order by advancing ‘model time’ to the time of the transaction at the head of the queue, removing that transaction from the queue and processing it. Processing a transaction will typically put another transaction in the queue, representing the next thing to be done for that bot, and the model continues processing the essentially endless queue of transactions in transaction time order until the model time reaches a preconfigured limit.

With a few exceptions, when the model processes a transaction that changes the balance of cash held by a bot, the model makes a decision as to whether and at what price the bot will endeavour to buy or sell goo as a function of the bot’s cash balance and the last traded price, ‘p’, of goo as per the following table:

Bot's cash balance (b)	Sell amount (globs)	Buy amount (globs)
b < $0	10,000 / p
$0 <= b < $5,000	5,000 / p
$5,000 <= b < $10,000	-	-
$10,000 <= b < $20,000		5,000 / p
$20,000 <= b		10,000 / p

The exceptions are that if a bot already has an outstanding order, a second order is not placed. Instead when the original order is concluded, consideration is given to placing another order in accordance with the above table. Additionally, if the bot has less goo than the amount of goo to be sold, the amount to be sold is reduced to the amount of goo that the bot has.

When selling goo, the bot first sets a sale price equal to 1.05 times the last sale price of goo. It then sells goo to the buyers already in the market who are offering to buy goo at prices equal to or higher than the bot’s sale price. Any remaining unsold goo is put on the market at the sale price to wait for a subsequent buyer. If no buyer purchases the goo within a randomly selected order expiry time between 0.8 and 1.2 days, the original order expires and provided the original cash balance conditions are still satisfied, the bot sets a new sale price at 99.5% of the previous order price or 1.05 times the last sale price of goo, whichever is less, and repeats the entire process, progressively discounting the order until all the goo is sold.

Similarly, when buying goo, the bot first sets a buying price equal to 0.95 times the last sale price of goo. It then purchases goo from the sellers already in the market who are offering to sell goo at prices equal to or less than the bot’s buying price. Any remaining unpurchased goo is put on the market at the buying price to wait for a subsequent seller. If no seller supplies the goo within a randomly selected order expiry time between 0.8 and 1.2 days, the original order expires and provided the original cash balance conditions are still satisfied, the bot sets a new buying price at 100.5% of the previous order price or 0.95 times the last sale price of goo, whichever is greater, and repeats the entire process, progressively increasing the buying price until all the required goo is purchased.

The sale and purchase of goo in situations where a bot is willing to sell goo at a price lower than another bot is willing to buy it, is resolved according to the order in which the sell and buy orders were placed. If the sell order is placed first, the buying bot will accept the seller’s price before placing an order for the remainder at the buying price. Conversely, if the buy order is placed first, the selling bot will sell goo at the buyer’s price before placing an order for any remainder at the selling price.

Growing Money Supply

To emulate the effect of a growing money supply, each of 10,000 bots were configured to start off with a cash balance of $7,500 and 5000 globs of goo, which was initially priced at $1 per glob.

At randomly distributed intervals of between 28 and 32 days, each bot received a random normally distributed net handout after expenses with a mean of $1000 and a standard deviation of $5000.

Rather expectedly, the price of goo appreciated over four-fold as shown below:

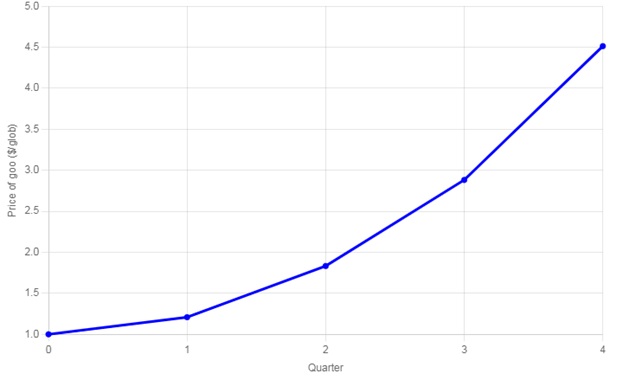
Price of Goo under a Growing Money Supply

In tabular form the results were:

Parameter	Initial value	After 365 days
Price of goo	$1.00/glob	$4.51/glob
Total net handouts given to the population of bots	$0.00	$118.25M
Total cash balance of the population of bots	$75.00M	$193.25M
Total quantitiy of goo held by the population of bots	50.00 M-globs	50.00 M-globs
Total value of goo held by the population of bots	$50.00M	$225.65M

The $118.25M injected into the economy is still in the economy and has simply been added to the $75.00M of initial cash to create the $193.25M final cash balance.

Further, the perceived wealth of the population has increased as follows:

Parameter	Initial value ($M)	After 365 days ($M)
Total wealth in cash	75.00	193.25
Total wealth in goo	50.00	225.65
Total perceived wealth	125.00	418.90

The difference between the initial and final total perceived wealth is $293.90M which is considerably greater than the $118.25 of additional cash injected into the economy. It is worth noting at this point that goo has no utilitarian function and that the increase in wealth associated with its apparent escalation in value is entirely illusory, except, of course, for those bots lucky enough to convert it into cash at the prevailing high price.

The Source of Asset Price Appreciation

The question that arose from the first experiment was whether it was actually necessary for money to be injected into the economy in order to provoke asset price appreciation, or whether it was sufficient for the float to simply be greater than a determinable threshold above which asset prices appreciated spontaneously?

To make this determination, the population of 10,000 bots were each initiated with an equal amount of cash. In separate runs of the model, the amount of cash was varied between $5,000 and $10,000 per bot.

To inject some background activity into the model, the bots were programmed to simulate trading between each other by the random transfer of cash from one bot to another. These transfers were programmed to occur at a randomly selected inter-transfer intervals of between 8 and 26 seconds. The values of the transfers were normally distributed with a mean of $200 and a standard deviation of $100. If the value of the transfer exceeded the cash balance of the transferor, it was reduced to the amount of the cash balance of the transferor.

The results were as set out below:

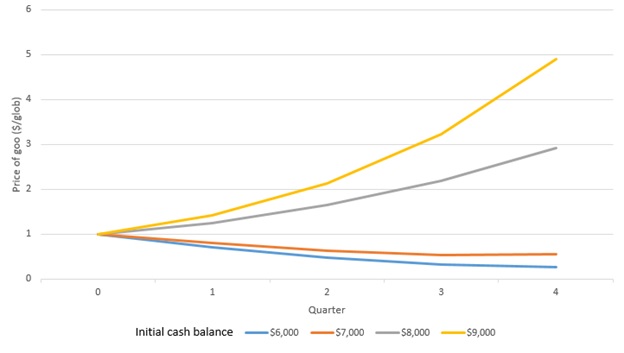
Price of Goo as a Function of Initial Cash Balance

It rather seemed that there might be an unstable equilibrium somewhere between an initial balance of $7,000 and $8,000 at which the price of goo neither increases nor decreases. However, when the model is allowed to run for a longer period of time something somewhat unexpected happened, which is the subject of the next experiment.

What Happens with Longer Runs?

To investigate what happens with longer runs, the configuration in the previous experiment with an initial cash balance of $6,000 per bot was allowed to run for a period of 3 simulated years.

The results were as follows:

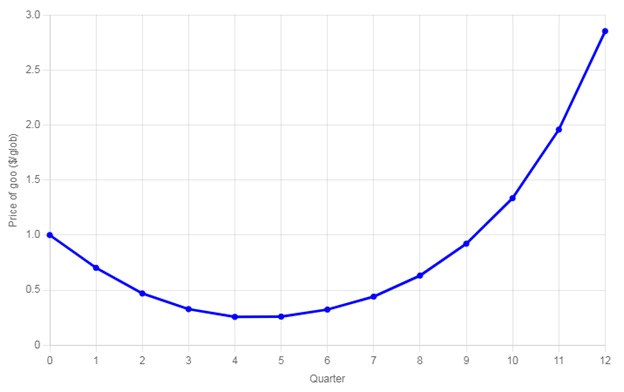
Price of Goo over Time with Initial Cash Balance of $6,000

What is particularly curious is that although the price of goo depreciates for the first 4 quarters, it subsequently appreciates in a manner similar to what happens when the initial cash balance per bot is higher than the imagined equilibrium.

A scatter plot of the cash and goo balances at the end of the 3-year run is presented below 2 and a frequency distribution of the cash balances of bots with no goo (which show as a line along the horizontal axis of the scatter plot) is presented below that.

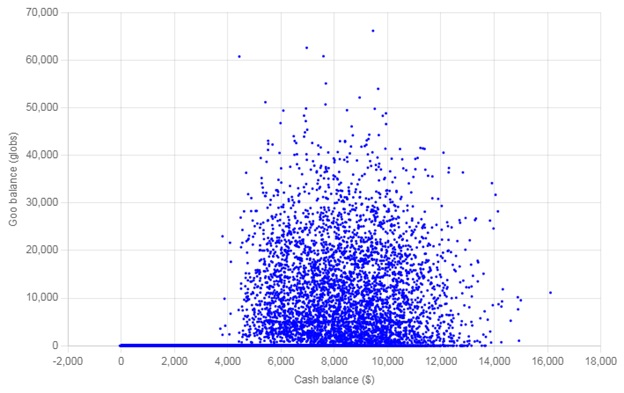
Scatter Plot of Bot Balances after 3 Years

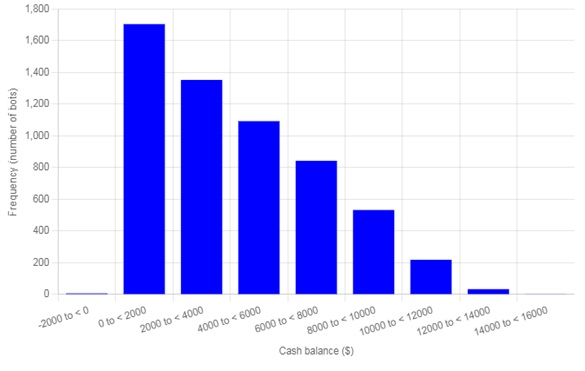
Cash Balances of Bots with no Goo

It seems that what happens in this situation is that the bots separate into two groups. One with sufficient cash and goo to provoke asset price appreciation and another with members having no goo and cash balances mostly insufficient to buy any – essentially, they’re impoverished.

Monetary Tightening

As a final experiment, the model was programmed to set the initial cash balance per bot to $8,000 and then after one year to reduce the cash balance per bot by $1,000, to emulate the effect, say, of a hawkish central bank.

The results were as follows:

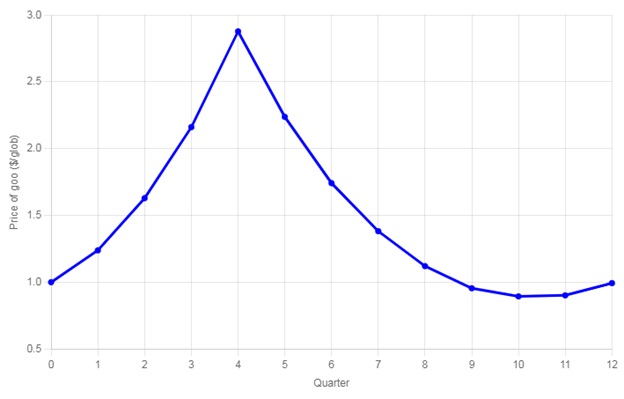
Tightening Money Supply after One Year

Rather as one would expect, the initial tightening of the money supply forces the less well-off bots to sell their goo, which depresses the price, but once those bots are excluded from the trading population and the money supply stabilises, the price restarts its upward trend.

So what does all this Mean?

If a population ever gets itself into a state in which there exists a belief that a certain commodity is more desirable than cash, so long as there is a surplus of cash in the economy and the market for the commodity remains liquid, it rather seems that the price of the commodity will appreciate. The appreciating price of the commodity is likely to reinforce the belief that the commodity is more desirable than cash and so perpetuates the appreciation.

The asset price appreciation does not require a continual increase in the money supply because although the price of the traded commodity increases, the increasing price does not remove money from the economy. It merely transfers money from one participant to another. All that is required for the appreciation to persist is that the amount of money available in the economy is sufficient to provide a surplus for investment.

Even if the average amount of money in the economy is insufficient to provide a surplus for investment, the participants in the economy are likely to divide into two groups, one with sufficient money to invest in the commodity, whose perceived wealth perpetually increases, and another that is at least somewhat impoverished. If this is as true in reality as it appears to be in the simplistic world of the present model, the consequences for the poor in societies that entertain distractions such as cryptocurrencies would seem to be quite sad.

In an economy with an appreciating commodity price, if circumstances should change so that cash becomes tight (for example, as a consequence of central bank tightening), the price of the commodity decreases, at least initially.

At the time of writing, central banks around the world are tightening the money supply to fight inflation. I would consequently conclude that the outlook for gooey assets is, at least until the central banks stabilize their tightening, somewhat negative, but once the money supply stabilises and assuming that the population or a meaningful proportion of it continues to believe that gooey assets are more desirable than cash, then I think we can expect the prices of gooey assets to start rising again.

Of course, the ultimate threat to gooey assets is popular disillusionment with the asset itself. If a population ever abandons its belief that a gooey asset is more desirable than cash, then I should think that the decline in price would be most catastrophic, but that will need to be the subject of a future investigation.

© 2022 Jonathan Searcy